epis Education Centre 教室案内
4SY 冬期講習第1回 7月8日(月) 授業報告
算数

夏期休講中の宿題
夏期テキスト p.88~ 小数のかけ算・わり算
小数のかけ算は、たし算・ひき算と違って、ひっさんの時に小数点をそろえる必要がありません。
その後、問題の2つの数字の小数点がずれている個数だけ合わせて、答えの小数点をずらします。
小数のわり算は、「わる数が整数のとき」は、そのままわって、答えの小数点はわられる数の小数点の位置を使います。
「わる数が小数のとき」は、それを整数にするために小数点をずらし、それと同じだけわられる数の小数点をずらします。
【宿題】
*テキストには書き込まず、ノートに書いて計算しましょう。
計算途中は必ず残しておいて、間違えたときにどこで間違えたのかを確認できるようにしておきましょう。
担当:東本(とうもと)
tohmoto@epis-edu.com
0708PEP Intermediate
英語
7月15日は冬期休講です。
Links
・Zoom・教材と宿題(Readingの答えもこちら)
↑通常とzoomリンクが異なります。ご注意ください。
【授業内容】
・Vocabulary
0708 VocabularyCheck
発音も正しく覚えていこう!Definitionも含めて使って覚える!
毎週板書には付属する情報もたくさん書いています!必ず板書はメモを取ること!
きちっと覚えて使ってみよう!だんだん語彙も難しくなってきましたね。
・Writing
新テーマ
・Grammar
・新しく preposition (前置詞) が始まりました。
・prepositionのイメージや働きを整理していきましょう!
・Reading
問題に答えることはもちろん、知らない単語の意味調べや音読も欠かさないこと!
段落の働きについて考えること!
【宿題】
・Vocabulary:復習
・Writing:テーマ参照(Writing)
・Grammar:Intermediate §21 p.296 - 299, 302 + 欲しい人はあげます。
*Holiday Homework:§2 - 9 revision test のページ
・Reading:6Aの残りと復習 + プリント・音読
・Video:
担当 坂本
______________________________________________________________________________________
*単語学習について
Reading中で知らない単語や赤字になっている単語を中心に、まとめたり意味を調べたりしてください。自分でテストできるような形でまとめておくのが望ましいです。
*Writingについて
たくさん書くのではなく、まずは書ける範囲で、正確に書く努力をしてみましょう。
それができたら、表現を広げて、ReadingやVocabularyで習った単語も使ってみよう!
*宿題の達成度について
当講座の設置目標である、「書けるための英語力」を実践するためにも、Writing課題は欠かさずに実施してください。次に、テーマ力のためのReadingですね。語彙力向上も欠かせません。Grammarはこの中では優先順位が1番低いです。繰り返し学習しますので、1周目は他2分野+復習に時間を使ってもいいでしょう。
学習方法については適宜ご相談ください!
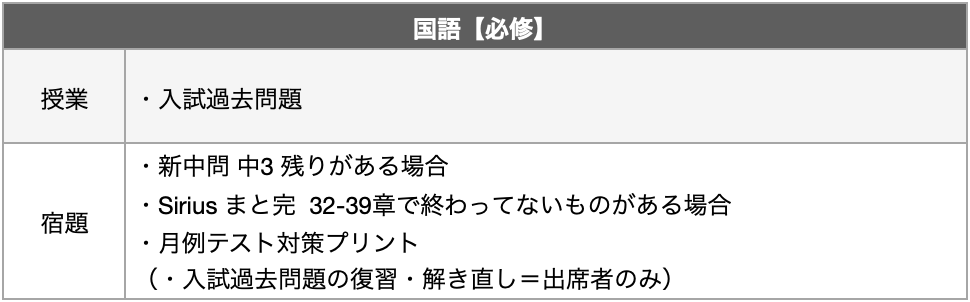
0708/0713 中3国語
カテゴリ
月別アーカイブ
- 2014年 5月 (1)